Overview
In this project I create a "morph" animation of my face into someone else's via a continuous morph of the image shape and cross-dissolve of the image colors. I proceed to compute the average face of a population (the IMM Face Database) and use it to extrapolate features of my own face and create caricatures of my features.
Part 1. Defining Correspondences
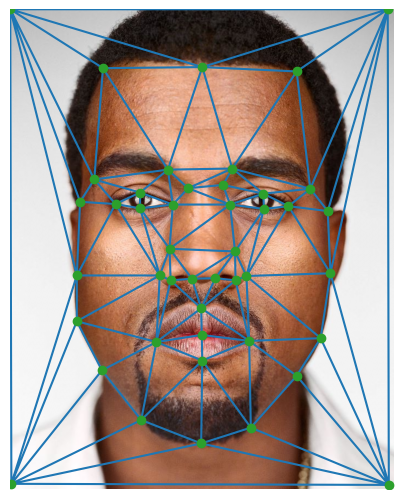
I crop and rescale a beautiful portrait of notorious American rapper Kanye "Ye" West (taken by Martin Schoeller) and a beautiful image of myself (taken by myself) to the same image size, attempting to match the facial size and aspect ratio to the best of my ability. I then used an online tool to manually label a total of 45 correspondences between the two images. These correspondences represent the locations of key features on each image that should map to each other.
After labelling the correspondences, I compute a Delaunay triangulation of each face to be used for morphing.
Correspondences and Delaunay Triangulation (45 points)

Part 2. Computing the "Mid-way Face"
We can compute the mid-way face by first computing the average shape (averaging each pair of correspondences in each image), warping images into that shape, and averaging the colors together by cross-dissolving.
In order to warp the images, I compute the inverse of the affine transformation matrix between each triangle in the original image and the corresponding triangle in the average shape. I then perform inverse warping with this matrix, performing bilinear interpolation in the case that the inverse transformation warps values between pixels, and iterate over all triangles to produce the warped image.



Part 3. The Morph Sequence
Using similar methodology to creating the mid-way face in the previous part, we can create a continuous morph from one image to the next by letting the shape warping fraction (e.g. 0.5 for mid-way) and cross-dissolve fraction vary with time. I create a gif of 100 frames each direction of this continuous morphing process, with 25 ms per frame, over a total of 5 seconds. Each fraction was scaled linearly with time.

Part 4. The "Mean face" of a population
I first compute the average shape of Danes in the IMM Face Database (consisting of 240 images of male and female Danes) by first parsing the correspondences in the database, then taking the average in order to get the mean shape.
Below are examples of images from the data set, followed by what their faces look like after being warped to the average Dane face.








After warping to the average face shape, I take the mean of all the images to get the mean face for all of the images in the dataset.

Next, I warp my face onto the average shape of Danes, and warp the average face onto my geometry. It looks a bit strange since the aspect ratios for our faces are quite off vertically, and the correspondences in the Dane dataset do not include forehead and hair.


Part 5. Caricatures - Extrapolating from the mean
Extrapolating my face shape from the Danish mean shape and vice versa, I can create caricatures of myself. The formula I use for extrapolation is p + alpha*(q - p), where p is a point on my face, q is a corresponding point on the population mean, and alpha is a variable scalar. alpha>1 corresponds to emphasizing the shape/geometry of the population mean, and alpha<0 corresponds to emphasizing my own geometry.


Bells & Whistles
Changing Gender
I found an image of an averaged Taiwanese female face from this website and experimented with using the image morphing techniques described above. I first morphed my facial geometry onto that of the average Taiwanese female, then compared it to cross-dissolving the images without morphing the geometry. Afterwards, I tried morphing both appearance and shape, and I believe it looks the best. Honestly, if I were real I would date me.





Roommate Morphing Music Video
I made an image morphing music video of my roommates and I that can be found below:
Principal Component Analysis
We can reshape the image matrices in the Danes dataset as vectors, and perform Principal Component Analysis on the matrix of all of them to obtain the principal components for the dataset. I choose to do this after geometrically reshaping the faces in the images, so that the resulting vectors mostly contain color information. A picture of the top 16 principal components is displayed below, from highest to lowest left to right top to bottom.

I proceed to reconstruct some of the images from the dataset using 16 principal components and 100 principal components, reconstruct the average face in the basis, and also attempt to reconstruct my face in the basis.


















As can be seen above, more principal components captures more of the color and details. The details seem to be captured on the edges first, which makes sense as there is a lot of variation in the center where the faces are that makes it difficult to capture. My face also is not represented well by the basis, but this is partially due to it being so far out of distribution compared to the other faces.